Elementary combinatorics and cryptanalysis
Why would a mathematician interested in combinatorics and cryptanalysis named lynne marie butler post the list below?
a lenient mulburry
tell riemann buyer
eat blurry linemen
eminent blurry ale
brainy menu teller
rumble realty nine
berlin realty menu
ninety mule barrel
mull binary entree
ninety marble rule
miller bunyan tree
eerily mental burn
I’m about to tell you the answer, so delay reading on if you want to figure it out yourself. Each row of the list is a permutation of the multiset of letters in her name, and both combinatorics and cryptanalysis start with the study of permutations. The multiset that is being permuted has type (3,2,2,2,2,1,1,1,1,1,1,1) because each row has 3 e’s, 2 l’s, 2 n’s, 2 r’s, 2 blanks, and 1 each of the other 7 letters. (Curtis Greene can do this to your name. You can read more about elementary combinatorics in Brualdi’s Introductory combinatorics, and cryptanalysis in Sinkov’s Elementary Cryptanalysis: a mathematical approach. My favorite advanced texts on these subjects are Stanley’s Enumerative combinatorics, and Koblitz’s A course in number theory and cryptography.)
Order analogues
The subsets of a multiset of type (2,2,1) may be visualized using the diagram shown below at right. (Under inclusion, these subsets form a partially ordered set; the diagram shown is its Hasse diagram.) Likewise, the subgroups of the group Z/4Z x Z/4Z x Z/2Z may be visualized using the diagram shown below at left. This group is a finite abelian p-group of type (2,2,1), for the prime p=2.
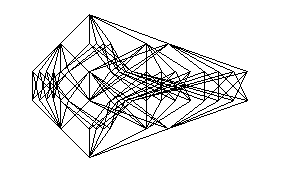
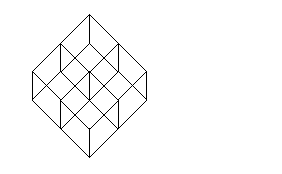
An order-preserving surjection that relates subgroups of a finite abelian p-group of type µ and subsets of a multiset of type µ is illustrated by the animation you’ll see if you click anywhere on the subgroup lattice shown above. This surjection is defined in my paper Order analogues and Betti polynomials. The animation that illustrates the case µ = (2,2,1) and p=2 was produced with the help of Toby Orloff, using software developed by the Geometry Center. It suggests that if [µ,k] is the number of subgroups of order pk in a finite abelian p-group of type µ, then
[(2,2,1),5] = 1
[(2,2,1),4] = 1 + p + p2
[(2,2,1),3] = 1 + p + 2 p2 + p3
[(2,2,1),2] = 1 + p + 2 p2 + p3
[(2,2,1),1] = 1 + p + p2
[(2,2,1),0] = 1
because there is 1 subgroup at the top level 5, 1+2+4 subgroups at level 4, 1+2+2(4)+8 subgroups at levels 3 and 2, 1+2+4 subgroups at level 1, and 1 subgroup at the bottom level 0. In my first paper, A unimodality result in the enumeration of subgroups of a finite abelian group, I proved that [µ,k]≤[µ,k+1] if k < n/2 and µ is a partition of n. The subgroup lattice doesn’t narrow as you move toward its middle level!